第2章感知机 coding

发表于 2023-07-15 更新于 2023-07-16 分类于知识库， AI ，机器学习，统计学习方法阅读次数：本文字数： 5.5k 阅读时长 ≈ 5 分钟

《统计学习方法》（李航第二版）课后习题及其代码实现

学习解析优秀的代码，源文件为.ipynb格式

代码来自github项目：fengdu78/lihang-code: 《统计学习方法》的代码实现 (github.com)

第2章感知机

1．感知机是根据输入实例的特征向量\(x\)对其进行二类分类的线性分类模型：

\[ f(x)=\operatorname{sign}(w \cdot x+b) \]

感知机模型对应于输入空间（特征空间）中的分离超平面\(w \cdot x+b=0\)。

2．感知机学习的策略是极小化损失函数：

\[ \min _{w, b} L(w, b)=-\sum_{x_{i} \in M} y_{i}\left(w \cdot x_{i}+b\right) \]

损失函数对应于误分类点到分离超平面的总距离。

3．感知机学习算法是基于随机梯度下降法的对损失函数的最优化算法，有原始形式和对偶形式。算法简单且易于实现。原始形式中，首先任意选取一个超平面，然后用梯度下降法不断极小化目标函数。在这个过程中一次随机选取一个误分类点使其梯度下降。

4．当训练数据集线性可分时，感知机学习算法是收敛的。感知机算法在训练数据集上的误分类次数\(k\)满足不等式：

\[ k \leqslant\left(\frac{R}{\gamma}\right)^{2} \]

当训练数据集线性可分时，感知机学习算法存在无穷多个解，其解由于不同的初值或不同的迭代顺序而可能有所不同。

二分类模型

\(f(x) = sign(w\cdot x + b)\)

\(\operatorname{sign}(x)=\left\{\begin{array}{ll}{+1,} & {x \geqslant 0} \\ {-1,} & {x<0}\end{array}\right.\)

给定训练集：

\(T=\left\{\left(x_{1}, y_{1}\right),\left(x_{2}, y_{2}\right), \cdots,\left(x_{N}, y_{N}\right)\right\}\)

定义感知机的损失函数

\(L(w, b)=-\sum_{x_{i} \in M} y_{i}\left(w \cdot x_{i}+b\right)\)

算法

随即梯度下降法 Stochastic Gradient Descent

随机抽取一个误分类点使其梯度下降。

\(w = w + \eta y_{i}x_{i}\)

\(b = b + \eta y_{i}\)

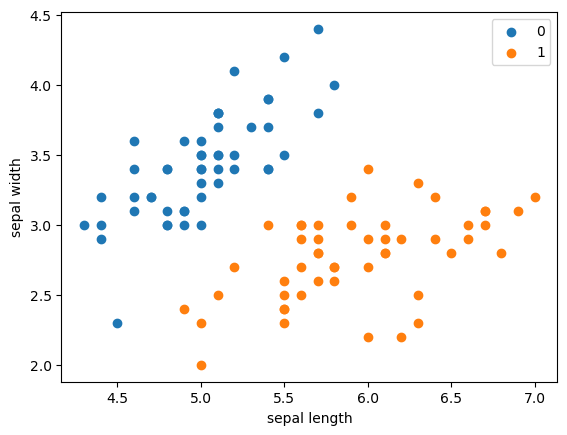
当实例点被误分类，即位于分离超平面的错误侧，则调整\(w\), \(b\)的值，使分离超平面向该无分类点的一侧移动，直至误分类点被正确分类拿出iris数据集中两个分类的数据和[sepal length，sepal width]作为特征

import pandas as pd  # 导入pandas库，用于数据处理和分析
import numpy as np  # 导入numpy库，用于数值计算
from sklearn.datasets import load_iris  # 从sklearn.datasets模块导入load_iris函数，用于加载鸢尾花数据集
import matplotlib.pyplot as plt  # 导入matplotlib.pyplot模块，用于绘图
%matplotlib inline  # Jupyter Notebook的魔术命令，将绘图结果直接嵌入Notebook中

iris = load_iris()  # 使用load_iris函数加载鸢尾花数据集，将返回的数据保存到变量iris中
df = pd.DataFrame(iris.data, columns=iris.feature_names)  # 创建一个DataFrame对象df，使用iris.data作为数据，iris.feature_names作为列名
df['label'] = iris.target  # 添加一个名为'label'的列，列数据为iris.target，表示鸢尾花的类别
df.columns = ['sepal length', 'sepal width', 'petal length', 'petal width', 'label']  # 重新设置DataFrame的列名
df.label.value_counts()  # 统计'label'列中各个类别的数量

plt.scatter(df[:50]['sepal length'], df[:50]['sepal width'], label='0')  # 绘制散点图，横轴为df中前50个样本的'sepal length'列，纵轴为df中前50个样本的'sepal width'列，标记为类别0
plt.scatter(df[50:100]['sepal length'], df[50:100]['sepal width'], label='1')  # 绘制散点图，横轴为df中50到100个样本的'sepal length'列，纵轴为df中50到100个样本的'sepal width'列，标记为类别1
plt.xlabel('sepal length')  # 设置横轴标签为'sepal length'
plt.ylabel('sepal width')  # 设置纵轴标签为'sepal width'
plt.legend()  # 添加图例

data = np.array(df.iloc[:100, [0, 1, -1]])  # 将df中前100行的'sepal length'、'sepal width'和'label'列提取出来，保存到变量data中
X, y = data[:, :-1], data[:, -1]  # 将data中的前两列作为特征矩阵X，最后一列作为目标变量y
y = np.array([1 if i == 1 else -1 for i in y])  # 将目标变量y中为1的标签替换为1，其余标签替换为-1，得到二分类的目标变量

Perceptron

# 数据线性可分，二分类数据
# 此处为一元一次线性方程

class Model:
    def __init__(self):
        self.w = np.ones(len(data[0]) - 1, dtype=np.float32)  # 初始化权重向量w，长度为特征数减1，初始化为全1
        self.b = 0  # 初始化偏置b为0
        self.l_rate = 0.1  # 学习率设置为0.1

    def sign(self, x, w, b):
        y = np.dot(x, w) + b  # 计算样本x与权重w的点积加上偏置b
        return y

    # 随机梯度下降法
    def fit(self, X_train, y_train):
        is_wrong = False
        while not is_wrong:
            wrong_count = 0
            for d in range(len(X_train)):
                X = X_train[d]  # 获取第d个样本特征向量
                y = y_train[d]  # 获取第d个样本的标签
                if y * self.sign(X, self.w, self.b) <= 0:  # 如果样本被错误分类
                    self.w = self.w + self.l_rate * np.dot(y, X)  # 更新权重向量w
                    self.b = self.b + self.l_rate * y  # 更新偏置b
                    wrong_count += 1
            if wrong_count == 0:
                is_wrong = True
        return 'Perceptron Model!'

    def score(self):
        pass

perceptron = Model()  # 创建Perceptron对象
perceptron.fit(X, y)  # 使用训练集X和标签y训练感知器模型
x_points = np.linspace(4, 7, 10)  # 在4到7之间生成10个等间距的点作为横轴数据
y_ = -(perceptron.w[0] * x_points + perceptron.b) / perceptron.w[1]  # 根据感知器模型的权重和偏置计算对应的纵轴数据
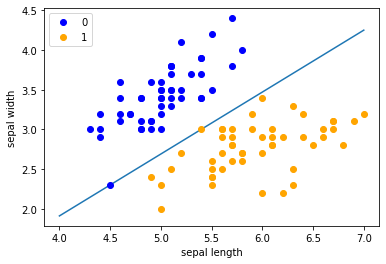
plt.plot(x_points, y_)  # 绘制分类边界线

plt.plot(data[:50, 0], data[:50, 1], 'bo', color='blue', label='0')  # 绘制类别0的样本点，蓝色圆点
plt.plot(data[50:100, 0], data[50:100, 1], 'bo', color='orange', label='1')  # 绘制类别1的样本点，橙色圆点
plt.xlabel('sepal length')  # 设置横轴标签为'sepal length'
plt.ylabel('sepal width')  # 设置纵轴标签为'sepal width'
plt.legend()  # 添加图例

scikit-learn实例

import sklearn  # 导入sklearn库
from sklearn.linear_model import Perceptron  # 从sklearn.linear_model模块导入Perceptron类
sklearn.__version__  # 输出sklearn库的版本信息

clf = Perceptron(fit_intercept=True, max_iter=1000, shuffle=True)  # 创建Perceptron对象clf，设置相关参数
clf.fit(X, y)  # 使用训练集X和标签y训练感知器模型

print(clf.coef_)  # 输出特征权重
print(clf.intercept_)  # 输出截距

plt.figure(figsize=(10, 10))  # 设置画布大小

plt.rcParams['font.sans-serif'] = ['SimHei']  # 设置中文标题显示
plt.rcParams['axes.unicode_minus'] = False
plt.title('鸢尾花线性数据示例')  # 设置标题

plt.scatter(data[:50, 0], data[:50, 1], c='b', label='Iris-setosa')  # 绘制类别0的样本点，蓝色圆点
plt.scatter(data[50:100, 0], data[50:100, 1], c='orange', label='Iris-versicolor')  # 绘制类别1的样本点，橙色圆点

x_points = np.arange(4, 8)  # 生成4到7之间的一组等差数列作为横轴数据
y_ = -(clf.coef_[0][0] * x_points + clf.intercept_) / clf.coef_[0][1]  # 根据感知机的权重和截距计算纵轴数据
plt.plot(x_points, y_)  # 绘制感知机的决策边界线

plt.legend()  # 显示图例
plt.grid(False)  # 不显示网格
plt.xlabel('sepal length')  # 设置横轴标签为'sepal length'
plt.ylabel('sepal width')  # 设置纵轴标签为'sepal width'
plt.legend()  # 显示图例

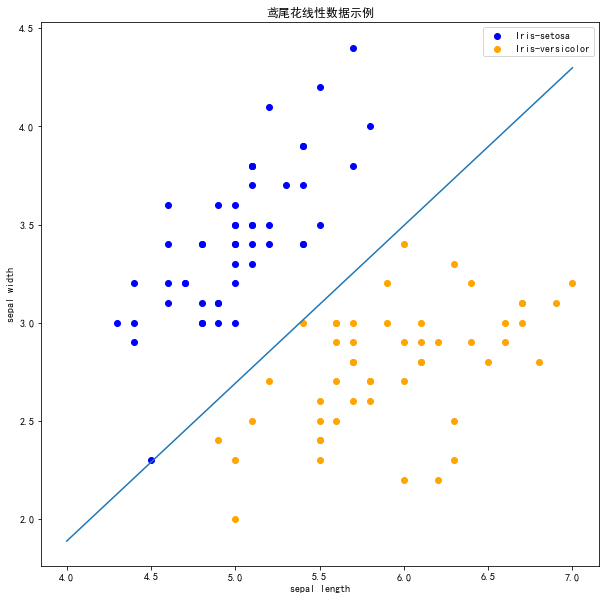
现在可以看到，所有的两种鸢尾花都被正确分类了。

第2章感知机-习题

习题2.1

Minsky 与 Papert 指出：感知机因为是线性模型，所以不能表示复杂的函数，如异或 (XOR)。验证感知机为什么不能表示异或。 总的来说，在二维坐标系上画出的点位无法感知机的线性分类器的一条线性函数正确划分，因此无法使用感知机。（或许采用非线性分类器可以？ 解答：

对于异或函数XOR，全部的输入与对应的输出如下：

\(x^{(1)}\)	\(x^{(2)}\)	\(y\)
1	1	-1
1	-1	1
-1	1	1
-1	-1	-1

参考代码：https://github.com/wzyonggege/statistical-learning-method

本文代码更新地址：https://github.com/fengdu78/lihang-code

习题解答：https://github.com/datawhalechina/statistical-learning-method-solutions-manual

中文注释制作：机器学习初学者公众号：ID:ai-start-com

配置环境：python 3.5+

第2章 感知机